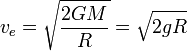Resumen de las experiencias con muelles.

1. ¿Cómo se deforma?
Tomamos medidas de la deformación del muelle al aplicarle fuerzas. Representamos en unos ejes (la deformación en el x) y obtenemos esta gráfica de excel. En el eje vertical está la fuerza en N, y en el eje horizontal la deformación en m.

La fuerza es proporcional a la deformación. la constante de proporcionalidad se escribe como k:


F = -k.x   k, en  nuestro experimento vale  17,64 N/m. El signo menos indica que la fuerza es contraria al desplazamiento. Es la llamada ley de Hooke de la deformación.

¿Cómo se mueve?
El movimiento del muelle es un movimiento periódico. Tarda un  tiempo T (periodo) en recorrer una oscilación completa.
Vamos a realizar experimentos para demostrar si:

¿El periodo depende de la amplitud?
Cogemos un muelle de constante k=17,6 N/m y lo cargamos con una masa de 230g. Le proporcionamos diferentes amplitudes de movimiento y medimos el periodo:

Amplitud (cm)	Periodo (s)
1	0,72
2	0,72
3	0,71
4	0,72

   Vemos que el periodo de un muelle no depende de la amplitud.

¿El periodo depende de la k?

Usamos varios muelles con constantes diferentes. En realidad acoplamos varios muelles en serie o utilzamos la mitad de uno. De esta forma conseguimos muelles de constantes diferentes. Usamos siempre la misma masa (250g) y la misma amplitud:

k (N/m)	Periodo (s)
17,64	0,75
8,82	1,06
5,87	1,3
35,28	0,53

El periodo disminuye al aumentar k
Esta disminución no es proporcional.
La relación entre T y k debe ser alguna función potencial inversa.
Los científicos prueban funciones hasta encontrar una que se ajuste a sus medidas.
Hemos encontrado que la constante es proporcional a 1/T2, o lo que es lo mismo que el periodo depende de la raíz de 1/k.

¿El periodo depende de la masa?

Cogemos un muelle de constante 17,64 N/m y le colgamos diversas masas. Medimos el periodo:

Periodo (s)	masa (kg)
0,58	0,15
0,67	0,2
0,75	0,25
0,82	0,3
0,88	0,35
0,95	0,4
1	0,45
1,06	0,5

El periodo aumenta con la masa pero no de forma proporcional. Al igual que antes probamos con diferentes funciones y encontramos que la masa está relacionada con T2, es decir que T depende de la raíz de m

CONCLUSIONES FINALES.

El periodo no depende de la amplitud.

El periodo depende de la raíz de m.

El periodo depende de la inversa de la raíz de k.

fotos

Las notas han sido:
5; 5,5; 6,8; 7,4; 7,5; 8;  8,4; 8,5; y 10

Cada uno que escoja lo que quiera,   a seguir bien.

Otro examen y algunas cositas

la basura espacial es 

un problema:

El increíble viaje del Voyager:

Un estupendo documental sobre el sistema solar.

Al final de los apuntes hay problemas con soluciones. Intenta los que quieras.

Otro examen sacado de Internet.

1- Se tienen dos masas puntuales de valores 3 y 5 Kg, colocadas en los vértices de la  hipotenusa de un triángulo rectángulo de catetos 30 y 40cm. Calcular el campo gravitatorio en el otro vértice.

Calcular el trabajo necesario para que otra masa de 2 Kg se mueva desde el punto A hasta el

punto B de coordenadas (40, 30) cm..

DATOS: G = 6,67.10-11 Unidades del sistema internacional

2- Se ha descubierto un planeta esférico de 4100 km de radio y con una aceleración de la

gravedad en su superficie de 7,2 m. s^-2

. a) Calcule la masa del planeta.

b) Calcule la energía mínima necesaria que hay que comunicar a un objeto de 3 kg de masa para lanzarlo desde la superficie del planeta y situarlo a 1000 km de altura de la superficie.

3-Un satélite artificial está situado en una órbita circular en torno a la Tierra a una altura de su superficie de 2500 km. Si el satélite tiene una masa de 1100 kg:

 a) Calcule la energía cinética del satélite y su energía mecánica total.

b) Calcule el módulo del momento angular del satélite respecto al centro de la Tierra y su periodo.

Datos: G, Masa de la tierra  y radio de la Tierra.

4- Un satélite de 1000 kg de masa describe una órbita elíptica alrededor de la Tierra. Cuando está a una distancia de 12000 km respecto del centro de la Tierra, su velocidad es de 3000 m/s. Calcule:

a) Su velocidad cuando la distancia al centro de la Tierra sea de 2.104 Km

b) la energía mecánica del satélite en la órbita.

Datos G, Mt,

5- Io, un satélite de Júpiter, tiene una masa de 8,9×10²² kg, un periodo orbital de 1,77 días, y un radio medio orbital de 4,22×10⁸ m. Europa es otro satélite de masa 4,8×1022 Kg, y un radio medio orbital de 6,71.10⁸ m. Considerando que las órbitas son circulares, determine:

a) La masa de Júpiter.

b) El periodo de Europa

 Datos: Constante de Gravitación G = 6,67×10-11 N m2 kg-2

.

 Radio de la Tierra = 6370 km.;

 Masa de la Tierra = 5,98×1024 kg.

Voyager - El viaje más lejano de la Humanidad

Otros posibles exámenes

examen del IEs TEROR.

OTRO EXAMEN DEL IES TEROR

recordar es importante publicar aquí las soluciones.

examen comenzado en clase

Examen del IES Veredillas.

EXAMEN FÍSICA 2º BACHILLERATO – TEMA 1: CAMPO GRAVITATORIO

OPCIÓN A

Cuestión 1.-

a) Desde la superficie de la Tierra se lanza verticalmente hacia arriba un objeto con una velocidad v. Si se desprecia el rozamiento, calcule el valor de v necesario para que el objeto alcance una altura igual al radio de la Tierra

b) Si se lanza el objeto desde la superficie de la Tierra con una velocidad doble a la calculada en el apartado anterior ¿escapará o no del campo gravitatorio terrestre?

Datos: Constante de Gravitación G = 6,67 × 10-11 N · m2 · kg-2 

Masa de la Tierra MT = 5,98 × 1024 kg  Radio medio de la Tierra RT = 6370 km

Cuestión 2.- Llamando g₀  a la intensidad de campo gravitatorio  determine en función del radio de la Tierra la altura sobre la superficie terrestre a la cual la intensidad de campo  gravitatorio es g₀/2

Cuestión 3.- Sabiendo que la aceleración de la gravedad en un movimiento de caída libre en la superficie de la Luna es un sexto de la aceleración de la gravedad en la superficie de la Tierra y que el radio de la Luna es aproximadamente 0,27 R_T (siendo R_T el radio terrestre), calcule:

a) La relación entre las densidades medias    D_luna/ D_tierra

b) La relación entre las velocidades de escape de un objeto desde sus respectivas superficies

V_{eLuna /}V_eTierra

Problema 1.- La velocidad angular con la que un satélite describe una órbita circular en torno al planeta Venus es ω₁= 1,45· 10^-4 rad/s y su momento angular respecto al centro de la órbita es L₁ = 2,2· 10¹² kg· m².s^-1. El momento angular o cinético se define (2º ley de kepler) como mvr.

a) Determine el radio r₁ de la órbita del satélite y su masa.

b) ¿Qué energía sería preciso invertir para cambiar a otra órbita circular con velocidad angular ω2 = 10^-4 rad/s?

Datos: Constante de Gravitación Universal G = 6,67· 10^-11N·m²·kg^-2

Masa de Venus Mv =4,87· l0²⁴ kg

Problema 2.- Un planeta esférico tiene 3200 km de radio y la aceleración de la gravedad en su superficie es 6,2 m/s².  Calcule:

a) La densidad media del planeta y la velocidad de escape desde su superficie.

b) La energía que hay que comunicar a un objeto de 50 kg de masa para lanzarlo desde la superficie del planeta y ponerlo en órbita circular alrededor del mismo de forma que su periodo sea de 2 horas.

Datos: Constante de Gravitación G = 6,67 × 10^-11 N · m² · kg^-2

Cuestión 1.- Plutón describe una órbita elíptica alrededor del Sol. Indique para cada una de las siguientes magnitudes si su valor es mayor, menor o igual en el afelio (punto más alejado del Sol) comparado con el perihelio (punto más próximo al Sol):

a) momento angular respecto a la posición del Sol

b) momento lineal (cantidad de movimiento mv)

c) energía potencial

d) energía mecánica.

Cuestión 2.- Cuatro masas puntuales idénticas de 6 kg cada una están situadas en los vértices de un cuadrado de lado igual a 2 m. Calcule:

a) El campo gravitatorio que crean las cuatro masas en el centro de cada lado del cuadrado.

Cuestión 3.-

a) ¿Con qué frecuencia angular debe girar un satélite de comunicaciones, situado en una órbita ecuatorial, para que se encuentre siempre sobre el mismo punto de la Tierra?

b) ¿A qué altura sobre la superficie terrestre se encontrará el satélite citado en el apartado anterior?

Problema 1.- Fobos es un satélite de Marte que gira en una órbita circular de 9380 km de radio, respecto al centro del planeta, con un periodo de revolución de 7,65 horas. Otro satélite de Marte, Deimos, gira en una órbita de 23460 km de radio. Determine:

a) La masa de Marte.

b) El período de revolución del satélite Deimos.

c) La energía mecánica del satélite Deimos.

d) El módulo del momento angular de Deimos respecto al centro de Marte.

Datos: Constante de Gravitación Universal G; Masa de Fobos = 1,1×10¹⁶ kg

Masa de Deimos = 2,4×10¹⁵ kg

Problema 2.- La nave espacial Discovery, lanzada en octubre de 1998, describía en torno a la Tierra una órbita circular con una velocidad de 7,62 km · s ^-1.

a) ¿A qué altitud se encontraba?

b) ¿Cuál era su período? ¿Cuántos amaneceres contemplaban cada 24 horas los astronautas que viajaban en el interior de la nave?

Datos: Constante de Gravitación G; Masa de la Tierra M_T = 5,98 × 10²⁴ kg

Radio medio de la Tierra R_T = 6370 km

Soluciones en la página de Internet.

examen de cursos pasados

 Se puntuará publicar en el blog las respuestas al examen.

A) 2. puntos. En la figura se representan 5 planetas con su masa y tamaño relativo. Indica en cual de ellos es mayor la velocidad de escape y en cual es menor.

B) 3 puntos. Un satélite artificial está dando vueltas a la Tierra a una altura de 300 km en una órbita estable. Calcular  el tiempo que tarda en dar una vuelta y la velocidad que lleva.  G=6,67.10^-11    R_T=6370000    M_T=6.10^-24    todo en el Sistema Internacional.

C) 3 puntos.  En el futuro todo lo bueno y todo lo malo que tenemos en la Tierra lo exportaremos a otros planetas. Es posible que haya guerras en Marte. Si un soldado dispara un proyectil  de 4g de masa a 1000 m/s  en la superficie de Marte ¿Qué altura puede alcanzar?  M_m=   6.10²³Kg          R_M=   3200 Km 

D)  2 puntos Con los datos que hemos escribiendo en el examen:

¿A qué altura sobre la superficie de la Tierra la gravedad es igual a la existente en la superficie de Marte?

E) Enuncia las leyes de Kepler y demuestra la tercera usando la ley de gravitación.

Tarea para el lunes 8.

1. lee esta noticia 

¿Cual es la idea más importante de la noticia?. ¿Qué ideas están asociadas a ella?.

¿Qué es un satélite de papel?.

¿Qué se hace con un satélite en la órbita estacionaria cuando acaba su vida útil? ¿Por qué?

2. Selectividad.

Busca en la página del instituto de Colindres dos problemas de Junio y Septiembre de 2010 del tema de gravedad.

Velocidad de escape

1. Leer en un libro o en esta página de mis apuntes teoría sobre la velocidad de escape.

2. Demostrar que la velocidad de escape viene dada por estas fórmulas 

3. Problema de esta página con solución.

4. 2. La estronauta Sunita Willians participó desde el espacio en la maratón de Boston del año 2007 recorriendo la distancia de la prueba en una cinta de correr dentro de la estación espacial. Sunita completo la maratón  en 4h 23m y 46 s. La estación orbitaba a 338km sobre la superficie de la Tierra.

a) gravedad terrestre a esa altura.
b) energía potencial y total de Sunita sabiendo que su masa es 45 kg.
c) ¿Qué distancia habrá recorrido Sunita mientras estuvo corriendo?

tarea para el viernes

1. Una piedra de 2 kg está situada a 1000 km de altura sobre la Luna sin velocidad. Cae sobre su superficie.
¿Qué ocurrirá? ¿por qué?
¿Qué energía tiene arriba?
¿Qué velocidad tendrá cuando llega a la superficie?
Datos: Ml=6.10²²kg  Rl=1740km.

A 1000 km de altura no tiene velocidad y se ve atraída por la Luna. Cae con un movimiento acelerado. Conforme va cayendo tiene más aceleración ya que la fuerza aumenta. Al final choca con la superficie con una gran velocidad produciendo un cráter como los de la foto.

La gravedad en el descenso va aumentando. Por tanto no podemos utilizar la fórmula Ep=mgh. Debemos utilizar la fórmula Ep=-GMm/r

Arriba.  Energía potencial = -GMm/r= -6,67.10^-11. 6.10²² . 10 /(1740000+1000000)= -14,6.10⁶J

En el choque  Ec= 1/2.m.v2
   Ep (no es cero)  = -GMm/r= -6,67.10^-11. 6.10²² . 10 (1740000) = -23.10⁶J

La energía arriba debe ser igual a la energía abajo ya que no hay rozamiento

-14,6.10⁶J = 5v2 +-23.10⁶J          v= 1300 m/s  una velocidad enorme como suponíamos.





Después hemos planteado el problema teórico de la novela "De la Tierra a la Luna".
En cada objeto del Universo hay una velocidad llamada velocidad de escape, de tal valor que si un objeto alcanza esa velocidad abandona completamente la gravedad del objeto alejándose indefinidamente. Si el objeto es muy pesado la velocidad de escape es grande, pero por ejemplo en la Luna es de solo 6800 m/s y por tanto las moléculas de los gases poco a poco abandonan la gravedad de la Luna. la Luna tiene tan poca gravedad que no es capaz de retener a las moléculas de los gases.

¿Qué velocidad debe tener un objeto para abandonar indefinidamente la Tierra?

En la superficie de la Tierra el objeto tiene energía cinética y potencial:
-GMm/r + ½ . m .v²  = -6,67.10^-11.6.10²⁴.m/ 6370000 + ½.m.v<sup>2

Si quiero que llegue a una altura infinita con velocidad 0, su energía final será:</sup>
-GMm/r + ½ . m .v²  =-6,67.10^-11.6.10²⁴.m/∞ +½.m. 0  = 0 J

Igualando ambas expresiones     v=11600 m/s.

Si un objeto tiene esta velocidad en la Tierra abandona completamente la atracción de la Tierra y se pierde en el espacio. Si la velocidad es menor el objeto volverá a caer sobre la Tierra, bien en una caída vertical, o en caída parábolica o incluso se puede quedar en una órbita estable.



1.- Un satélite artificial de 500 kg de masa se mueve alrededor de un planeta, describiendo una
órbita circular de 42,47 horas y un radio de 419.000 km. Se pide:
1. Fuerza gravitatoria que actúa sobre el satélite
2. La energía cinética, la energía potencial y la energía total del satélite en su órbita.
3. Si por cualquier causa, el satélite duplica repentinamente su velocidad sin cambiar la
dirección, ¿se alejará este indefinidamente del planeta? Razonar la respuesta. Sugerencia: Calcular la energía en este caso.

Para mañana.

1. A qué altura habrá que situar un satélite de comunicaciones para que dé 50 vueltas a la Tierra cada día.

2. Ganímedes es el satélite más grande de Júpiter y del Sistema Solar. Tiene 5.262 km de diámetro y es mayor que Plutón y que Mercurio. Gira a unos 1.070.000 km del planeta en poco más de siete días. Otro satélite es Io: Tiene 3.630 km de diámetro y gira a 421.000 km de Júpiter. Su órbita se ve afectada por el campo magnético de Júpiter y por la proximidad de Europa y Ganímedes. Es rocoso, con mucha actividad volcánica. Su temperatura es de -143º.
¿Cuál es la masa de Júpiter? ¿Qué velocidad tiene el satélite Io.?